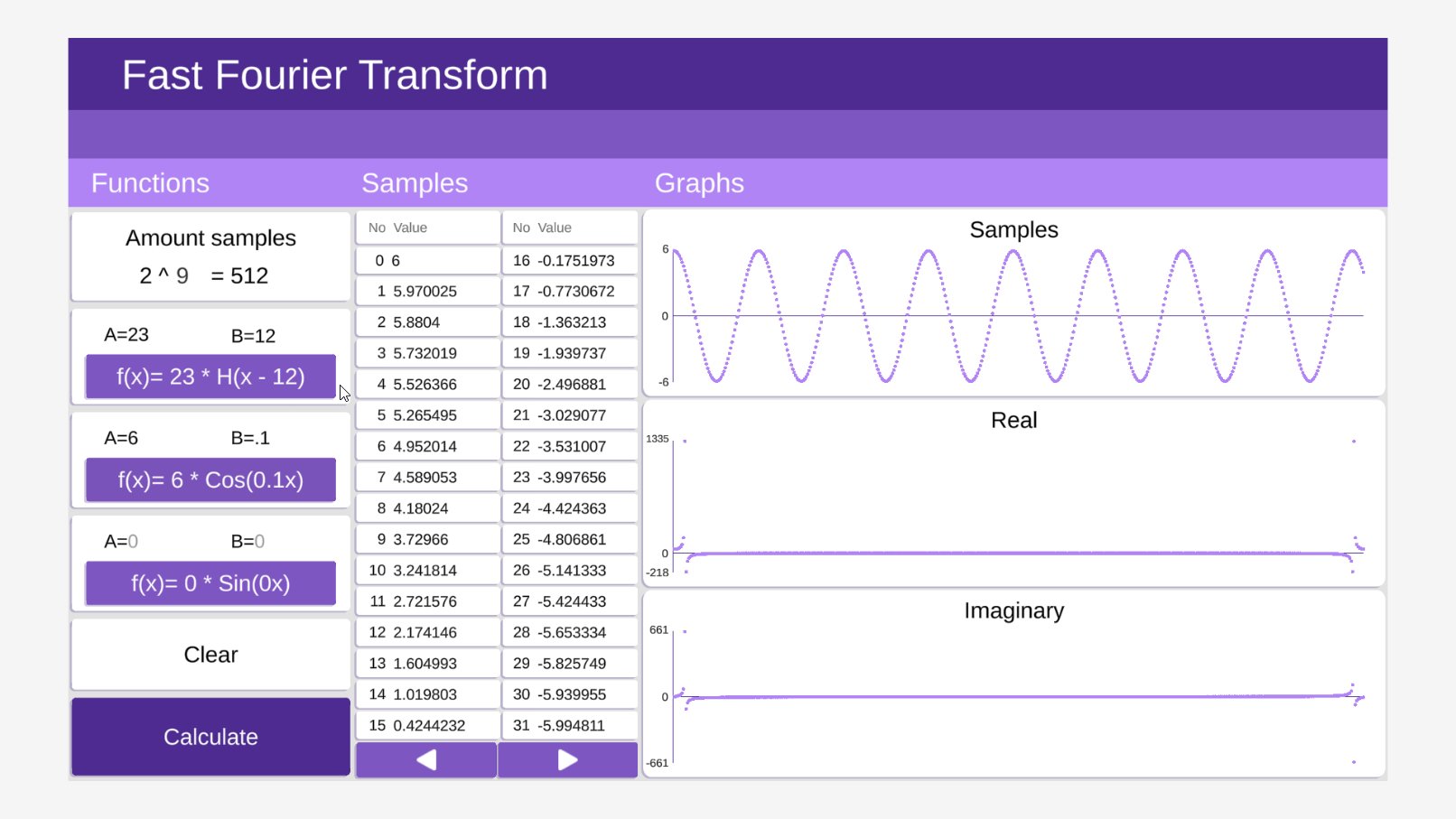
Efficient Fourier Transform Calculator: Your Essential Tool
Searching for a quick and accurate way to calculate Fourier transforms? Look no further – the Fourier transform calculator simplifies complex mathematical operations with just a few clicks. Transform your time domain data into frequency domain representations effortlessly, making analysis and signal processing a breeze. Save time and improve efficiency with this powerful digital tool that brings the complex world of Fourier transforms within easy reach. Dive into the world of digital signal processing and mathematics with the Fourier transform calculator by your side.
The Magic of Fourier Transform Calculator
Imagine unlocking the power to see the hidden secrets of the universe, like a magician revealing the mysteries of a magic trick. Well, that’s exactly what a Fourier Transform Calculator does – it unveils the hidden patterns behind the waves around us. In this blog post, we’ll dive into the world of Fourier Transform Calculators and discover how they work, why they are important, and how they can be used in everyday life.
What is a Fourier Transform Calculator?
Before we delve deeper into the fascinating world of Fourier Transform Calculators, let’s first understand what a Fourier Transform is. In simple terms, a Fourier Transform is a mathematical tool that allows us to break down a complex waveform into its individual frequencies. It’s like taking a piece of music and separating out the different notes that make up the melody.
Now, a Fourier Transform Calculator takes this mathematical concept and turns it into a user-friendly tool that anyone can use. With just a few clicks, you can input a waveform – such as a sound, image, or signal – and the calculator will perform the Fourier Transform for you, revealing the underlying frequencies.
How Does a Fourier Transform Calculator Work?
The inner workings of a Fourier Transform Calculator may seem complex at first, but fear not – we’re here to simplify it for you. Essentially, the calculator takes the input waveform and converts it from the time domain to the frequency domain. This transformation allows us to see the waveform in terms of its constituent frequencies, making it easier to analyze and understand.
One of the key components of a Fourier Transform Calculator is the Fast Fourier Transform (FFT) algorithm, which is like the engine that powers the calculator. The FFT algorithm efficiently computes the Fourier Transform of the input waveform, making it quick and easy for users to get results in a matter of seconds.
Why is Fourier Transform Calculator Important?
You might be wondering, why should I care about a Fourier Transform Calculator? Well, the answer lies in its versatility and practical applications. From music production to image processing, from telecommunications to medical imaging, Fourier Transform Calculators play a crucial role in a wide range of fields.
For example, in music production, Fourier Transform Calculators are used to analyze sound waves and create complex audio effects. By understanding the frequencies present in a piece of music, producers can fine-tune the sound to create the perfect mix.
Similarly, in image processing, Fourier Transform Calculators help reveal hidden patterns in images, making it easier to enhance and manipulate them. Whether it’s removing noise from a photograph or sharpening the details in a medical scan, Fourier Transforms are indispensable tools in the world of digital imaging.
How to Use a Fourier Transform Calculator
Now that you understand the importance of Fourier Transform Calculators, you might be eager to try one out for yourself. Luckily, using a Fourier Transform Calculator is easier than you think. Most online calculators have a simple interface where you can upload your waveform or enter it manually.
Once you input your waveform, the calculator will work its magic and display the results in the frequency domain. You’ll see a plot showing the amplitudes of different frequencies present in the waveform, allowing you to visually analyze the data.
Applications of Fourier Transform Calculators
The applications of Fourier Transform Calculators are vast and varied, spanning across different industries and disciplines. Let’s explore some of the common uses of these powerful tools:
1. Signal Processing
In signal processing, Fourier Transform Calculators are used to analyze and manipulate signals in fields such as telecommunications, audio processing, and radar technology. By decomposing signals into their frequency components, engineers can extract valuable information and enhance the quality of the signals.
2. Medical Imaging
In the field of medical imaging, Fourier Transform Calculators play a crucial role in technologies such as MRI (Magnetic Resonance Imaging) and CT (Computed Tomography) scans. These tools help physicians visualize internal structures within the body by analyzing the frequency content of the captured signals.
3. Speech Recognition
Speech recognition systems rely on Fourier Transform Calculators to analyze and process audio signals for converting speech into text. By identifying the unique frequencies present in spoken words, these systems can accurately transcribe spoken language into written text.
4. Astronomy
In astronomy, Fourier Transform Calculators are used to analyze the light spectra emitted by celestial objects. By breaking down the spectral lines into their constituent frequencies, astronomers can determine the composition and temperature of stars, galaxies, and other astronomical bodies.
In conclusion, Fourier Transform Calculators are truly magical tools that unlock the hidden patterns within the waves that surround us. From music production to medical imaging, from signal processing to astronomy, these calculators have revolutionized the way we analyze and understand the world around us.
So next time you hear about Fourier Transforms and Calculators, remember the magic they hold – the power to transform complex waveforms into beautiful frequencies that reveal the underlying secrets of the universe. Embrace the magic of Fourier Transform Calculators, and let the waves of knowledge wash over you!
ADVANCED ENGINEERING MATH FOURIER TRANSFORM
Frequently Asked Questions
What does a Fourier transform calculator do?
A Fourier transform calculator is a tool that performs mathematical operations to transform a signal or function from the time domain to the frequency domain. It helps analyze the frequency components present in a given signal and is commonly used in signal processing, engineering, and various scientific disciplines.
How can I use a Fourier transform calculator effectively?
To use a Fourier transform calculator effectively, you need to input the appropriate signal or function data in the required format. Make sure to understand the properties of the signal you are analyzing to interpret the results correctly. Additionally, learning about windowing functions and selecting the proper parameters is crucial for accurate results.
What types of Fourier transforms can be calculated using a Fourier transform calculator?
A Fourier transform calculator can perform various types of Fourier transforms, including the continuous Fourier transform, discrete Fourier transform (DFT), fast Fourier transform (FFT), and inverse Fourier transform. Depending on the application and input data, you can choose the appropriate type of Fourier transform to analyze the signal effectively.
Can a Fourier transform calculator handle complex signals or functions?
Yes, a Fourier transform calculator is capable of handling complex signals or functions by processing both real and imaginary components of the input data. It can accurately compute the frequency components of complex signals and provide insights into their spectral characteristics. Make sure to input the complex data in the correct format for precise results.
Final Thoughts
In conclusion, utilizing a Fourier transform calculator can simplify complex mathematical operations. This powerful tool allows for quick and accurate calculations in signal processing, image analysis, and other scientific fields. By inputting the desired function or data and selecting the appropriate parameters, users can efficiently obtain Fourier transform results. Embracing this technology can enhance research, problem-solving, and efficiency in various applications.


